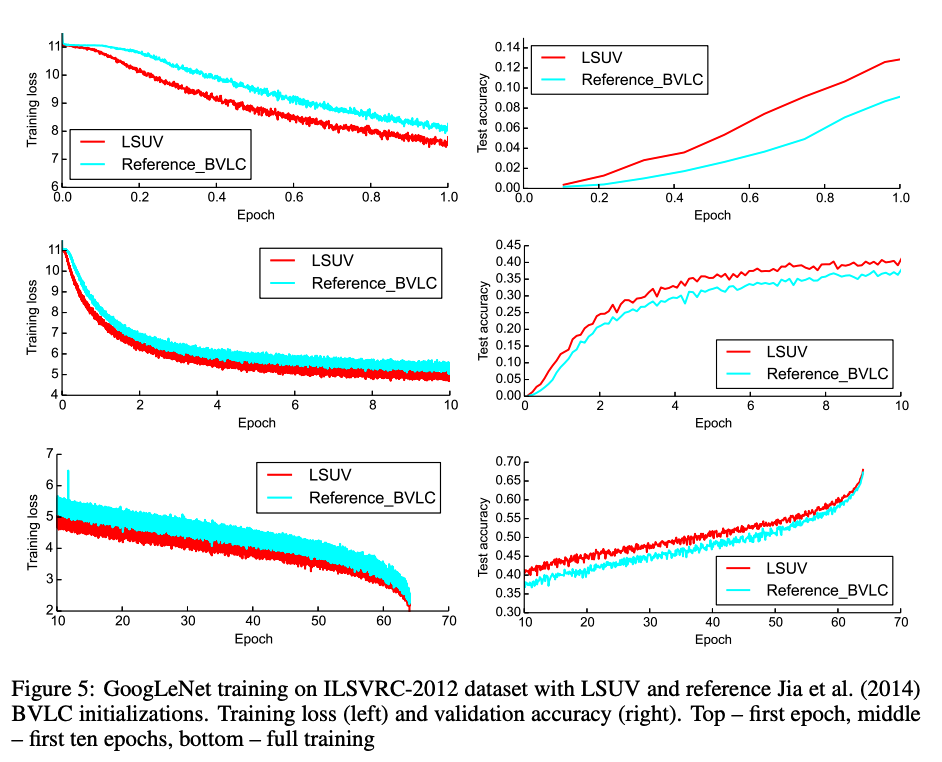
Image source : link
In 09_optimizer, the fastai introduces customized Optimizer class, which separates hyper-parameters from parameter groups so that we can easily adjust hyper-parameters. Comparing how the callbacks changed will help you understand difference between PyTorch optimizer and customizer Optimizer.
🎮📝 Q1. Implement your own version of Optimizer (as you did in minibatch), however, in this version, you use stepper function which was provided when initializing optimizer. Describe the motivation behind this brand-new optimizer.
🎮 Q2. Transform your general optimizer to SGD.
🎮 Q3. (optional) Adjust Recorder, ParamScheduler and LR_finder from dependency upon torch.optim to customized optimizer.
📝 Q4. Can you explain the main different apporoach between PyTorch Optimizer and customized Optimizer, using three modified callbacks: Recorder, ParamScheduler and LR_finder?
📝 Q5. See your model summary and parameters (e.g., opt_func.param_groups[0]['params']). Can you estimate how many paramters in your model from model summary (e.g., learn.model)?
📝 Q6. Explain the concept of weight decay and why does its concept connect to gradient descent.
🎮 Q7. Implement weight decay and l2 regularization using previously discussed information. And reimplement optimizer, which extracts hyper-parameters when compositional optimizing functions are given.
- Thought experimen: why do you think weght decay should come before sgd_step? Do you think the order of steppers are also important when applying l2 regularization?
🎮 Q8. Can you compare cosine schedulers of increasing period and decreasing period?
🎮 Q9. Now, test the flexibility of customized Optmizer. Can you change the step process (i.e., the way you update parameters.) as in Adam, Momentum, RMSProp without changing your model layers, parameters, dataset.. etc? Or can you fix hyperparameter you use without modifying others also? #TODO
📝 Q10. What is the role of a momentum when you manage a gradient?
🎮 Q11. Implement momemtum using customized Optmizer and see the training result.
- Hint: You will need
- object which initializes and updates moving average statistics
- modification on customized Optimizer to use newly added statistics
- actual stepper (just like sgd_step)
📝 🎮 Q12. Visualize the role of momentum with 1) randomly distributed data 2) generated data following specific formula. What do you see?
- Hint: when you test with a specific formula, set their first value to a different one. e.g.,
y[0]=0.7
📝 🎮 Q13. A term/trick debiasing comes into play in this context. Explain what is a debiasing, why do we need it, and how to do it. Explain both formula and implementation.
- Hint: see above plots, and try to find out common behavior fo momentum graph.
- Hint: modify
AverageGradand make dampening optional.
📝 🎮 Q14. Write down Adam optimizer formula (or process) - you don’t need to remember this. just peek up the paper. What do you think Adam’s major difference from momentum? Which additional processes need to be added to implement Adam from mometum? Implement those processes.
A1.
- Motivation: General optimizer which can adapt to any kind of optimizer. (c.f., pytorch defines the optimizer whenever new method comes out e.g., ASGD, AdamW, Adagrad, RMSprop …)
class Optimizer():
def __init__(self, params, steppers, **defaults):
self.param_groups = list(params)
# ensure params is a list of lists
if not isinstance(self.param_groups[0], list): self.param_groups = [self.param_groups]
self.hypers = [{**defaults} for p in self.param_groups]
self.steppers = listify(steppers)
def grad_params(self):
gps = []
for pg, hyper in zip(self.param_groups, self.hypers):
for p in pg:
if p.grad is not None:
gps = gps + [(p, hyper)]
return gps
def zero_grad(self):
for p, hyper in self.grad_params():
p.grad.detach_()
p.grad.zero_()
def step(self):
for p, hyper in grad_params:
compose(p, self.steppers, **hyper)
A2.
def sgd_step(p, lr, **kwargs):
# pytorch inplace function of sum. second parameter will be multiplied to first parameter
p.data.add_(-lr, p.grad.data)
return p
# steppers is compositional function
opt_func = partial(Optimizer, steppers=[sgd_step])
A3.
- Recorder: change in after_batch
class Recorder(Callback):
def begin_fit(self): self.lrs, self.losses = [], []
def after_batch(self):
if not self.in_train: return
self.lrs.append(self.opt.hypers[-1]['lr'])
self.losses.append(self.loss.detach().cpu())
def plot_lr (self, pgid=-1): plt.plot(self.lrs[pgid])
def plot_loss(self, skip_last=0): plt.plot(self.losses[:len(self.losses)-skip_last])
def plot(self, skip_last=0, pgid=-1):
losses = [o.item() for o in self.losses]
lrs = self.lrs[pgid]
n = len(losses)-skip_last
plt.xscale('log')
plt.plot(lrs[:n], losses[:n])
class ParamScheduler(Callback):
_order = 1
def __init__(self, pname, sched_funcs): self.pname, self.sched_funcs = pname, listify(sched_funcs)
def begin_batch(self):
if not self.in_train: return
fs = self.sched_funcs
"I don't know why we should multiply(i.e., copy) the number of pg here when (only) the length is one"
if len(fs) == 1:
print(f"before multiplying: {fs}")
fs = fs * len(self.opt.param_groups)
print(f"after multiplying: {fs}")
pos = self.n_epochs / self.epochs
for f, h in zip(fs, self.opt.hypers):
h[self.pname] = f(pos)
class LR_Find(Callback):
_order = 1
def __init__(self, max_iter=100, min_lr=1e-6, max_lr=10):
self.max_iter, self.min_lr, self.max_lr = max_iter, min_lr, max_lr
self.best_loss = 1e9
def begin_batch(self):
if not self.in_train: return
pos = self.n_iter / self.max_iter
lr = self.min_lr * (self.max_lr/self.min_lr) ** pos
# New
for pg in self.opt.hyper: pg['lr'] = lr
def after_step(self):
if self.n_iter >= self.max_iter or self.loss > self.best_loss*10:
raise CancelTrainException()
if self.loss < self.best_loss: self.best_loss = self.loss
A6. Weight decay is the way of peneltrating model from going (too) farther, implemented in loss. However, as it is inefficient to square and add to loss, we relocate it to optimization phase. 2 In results, weight decay is to subtract weight * lr * wd from weight. Which is same for L2 regularization, only in case you use SGD, adding weight * wd to the weight.grad
A7.
- In decoupled weight decay (i.e., AdamW) should apply sgd_step after weight decay, otherwise the weight decay will use ‘updated’ parameter value.
- This sequence is also applied to l2 regularization. See Decoupled Weight Decay Regularization - Algorithm.1 for more explaination.
def weight_decay(p, lr, wd, **kwargs):
p.data.mul_(1-lr*wd)
return p
weight_decay._defaults = dict({'wd':0.})
def l2_reg(p, lr, wd, **kwargs):
# p.g += lr*p
p.data.grad.add_(lr, p.data)
return p
l2_reg._defaults = dict({'wd':0.})
class Optimizer():
def __init__(self, params, steppers, **defaults):
self.steppers = listify(steppers)
self.param_groups = list(params)
maybe_update(self.steppers, defaults, get_defaults)
# ensure params is a list of lists
if not isinstance(self.param_groups[0], list): self.param_groups = [self.param_groups]
self.hypers = [{**defaults} for p in self.param_groups]
def grad_params(self):
gps = []
for pg, hyper in zip(self.param_groups, self.hypers):
for p in pg:
if p.grad is not None:
gps = gps + [(p, hyper)]
return gps
def zero_grad(self):
for p, hyper in self.grad_params():
p.grad.detach_()
p.grad.zero_()
def step(self):
for p, hyper in self.grad_params():
compose(p, self.steppers, **hyper)
def maybe_update(os, dest, f):
'''
os: optimizers
'''
for o in os:
for k, v in f(o).items():
if not k in dest: dest[k] = v
def get_defaults(o): return getattr(o, '_defaults', {})
A8
sched = combine_scheds(torch.tensor([.1, .2, .3, .4]), [sched_cos(0.8, .01), sched_cos(0.8, .01), sched_cos(0.8, .01), sched_cos(0.8, .01)])
learns, runs= get_learn_run(nfs, data, 0.4, conv_layer,
cbs=cbfs + [partial(ParamScheduler, pname='lr', sched_funcs=sched), Recorder],
opt_func = sgd_opt)
runs.fit(1, learn)
sched = combine_scheds(torch.tensor([.4, .3, .2, .1]), [sched_cos(0.8, .01), sched_cos(0.8, .01), sched_cos(0.8, .01), sched_cos(0.8, .01)])
learnf, runf= get_learn_run(nfs, data, 0.4, conv_layer,
cbs=cbfs + [partial(ParamScheduler, pname='lr', sched_funcs=sched), Recorder],
opt_func = sgd_opt)
runf.fit(1, learnf)
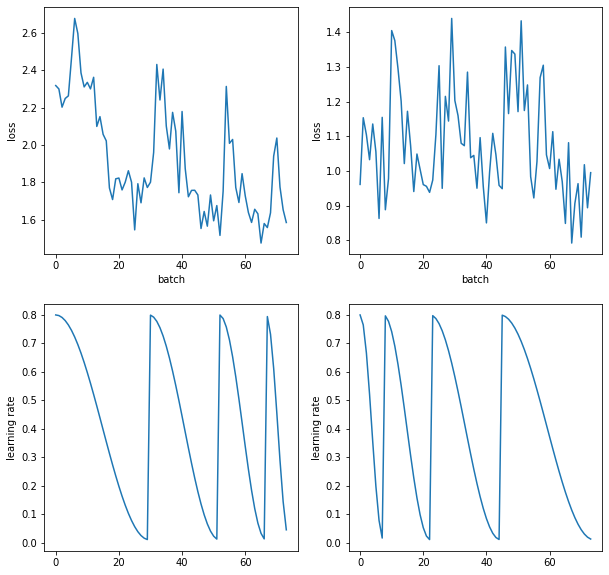
fig, axs = plt.subplots(2,2, figsize=(10, 10))
for ax, r in zip(axs.transpose(), [runf, runs]):
ax[0].plot([o.item() for o in r.recorder.losses])
ax[1].plot(r.recorder.lrs)
ax[0].set_xlabel('batch')
ax[0].set_ylabel('loss')
ax[1].set_ylabel('learning rate')
A9.
- To be done
A10. Giving a right direction is in the behind insight of the momentum. The right direction highly relies on the previous history. I think this concept is shared through the whole deep learning tricks, for example, batch normalization.3
A11.
class StatefulOptimizer(Optimizer):
def __init__(self, params, steppers, stats=None, **defaults):
self.stats = listify(stats)
maybe_update(self.stats, defaults, get_defaults)
super().__init__(params, steppers, **defaults)
self.state = {}
def step(self):
for p, hyper in self.grad_params():
# if state does not have p(parameter value) as its key, initialize
if p not in self.state:
self.state[p] = {}
# if training is in the first batch, initialize parameter filled in zeros
maybe_update(self.stats, self.state[p], lambda o: o.init_state(p))
state = self.state[p] # state = {'grad_avg': torch.zeros_like(p.grad.data)}
for stat in self.stats: state = stat.update(p, state, **hyper) # state = {'grad_avg': ((..... p-2.grad) * mom + p-1.grad) * mom + p.grad}
compose(p, self.steppers, **state, **hyper) # update parameter, i.e., p+1 = p - p * wd - p.g * lr
self.state[p] = state # assign state (i.e., update key as an updated parameter, value as an updated gradient)
class Stat():
_defaults = {}
def init_state(self, p): raise NotImplementedError
def update(self, p, state, **kwargs): raise NotImplementedError
class AverageGrad(Stat):
_defaults = dict(mom=0.9)
def init_state(self, p):
return {'grad_avg': torch.zeros_like(p.grad.data)}
def update(self, p, state, mom, **kwargs):
state['grad_avg'].mul_(mom).add_(p.grad.data)
return state
def momentum_step(p, lr, grad_avg, **kwargs):
p.data.add_(-lr, grad_avg)
return p
sgd_mom_opt = partial(StatefulOptimizer, steppers = [momentum_step, weight_decay], stats=AverageGrad(), wd=0.01)
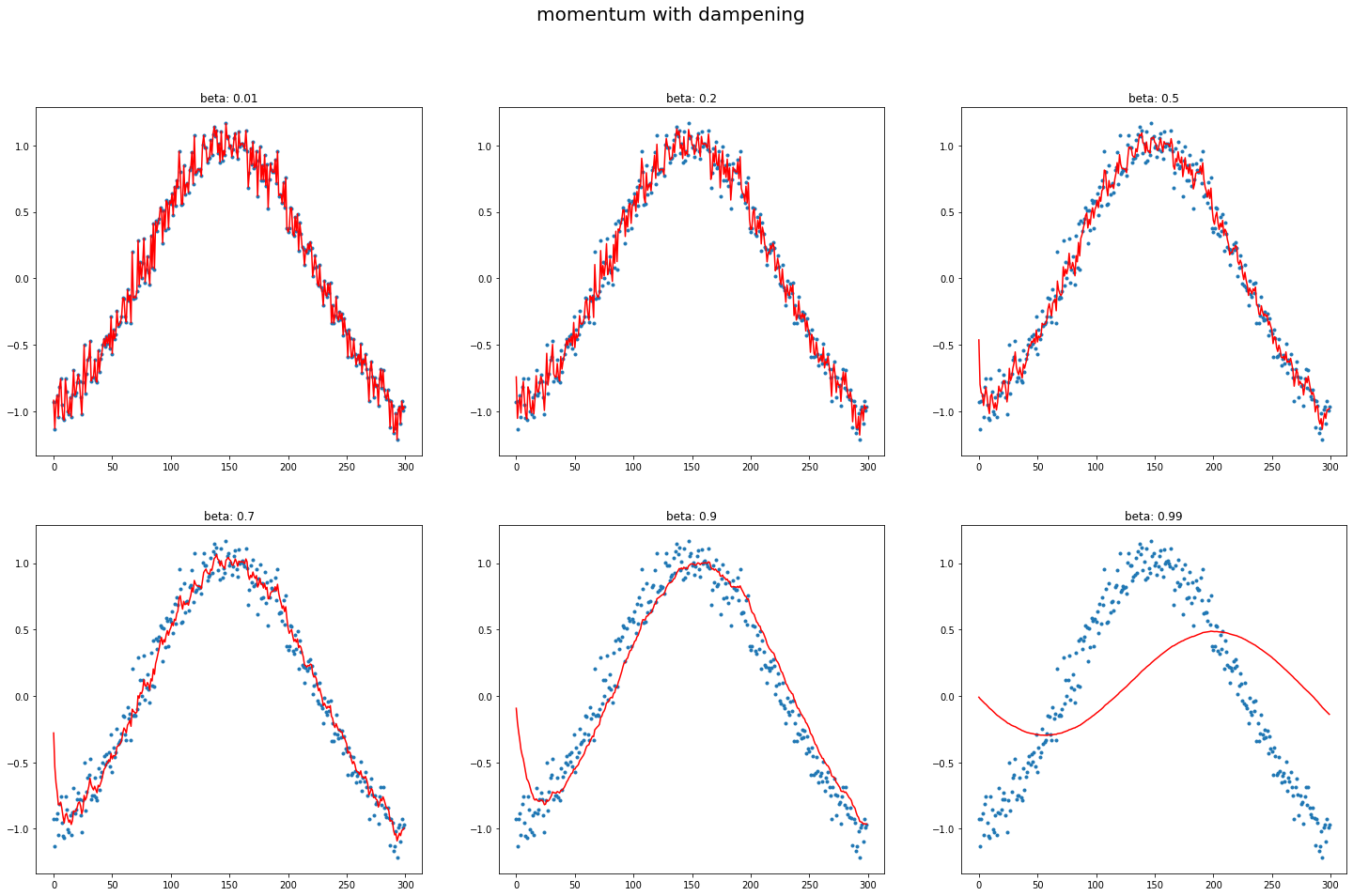
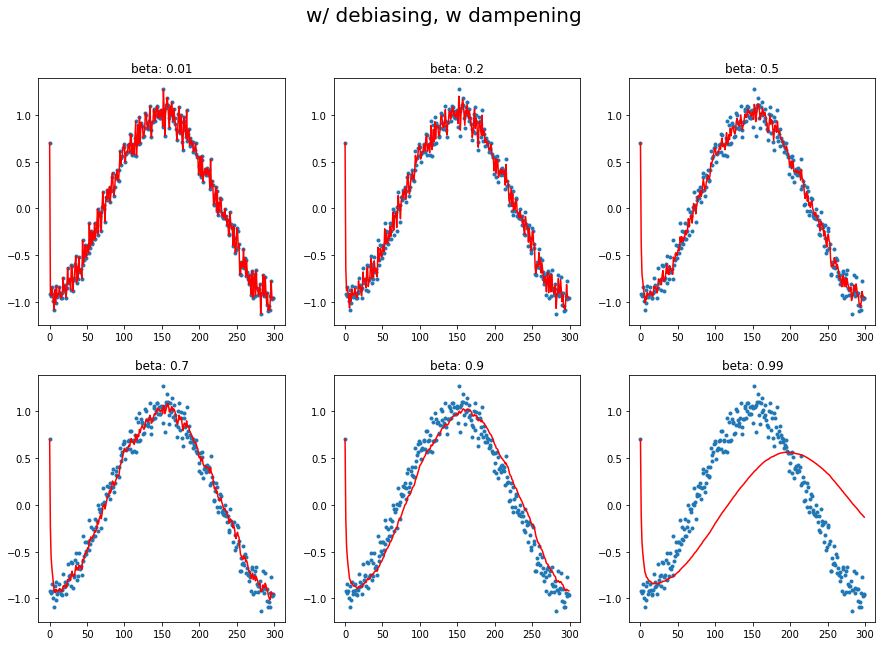
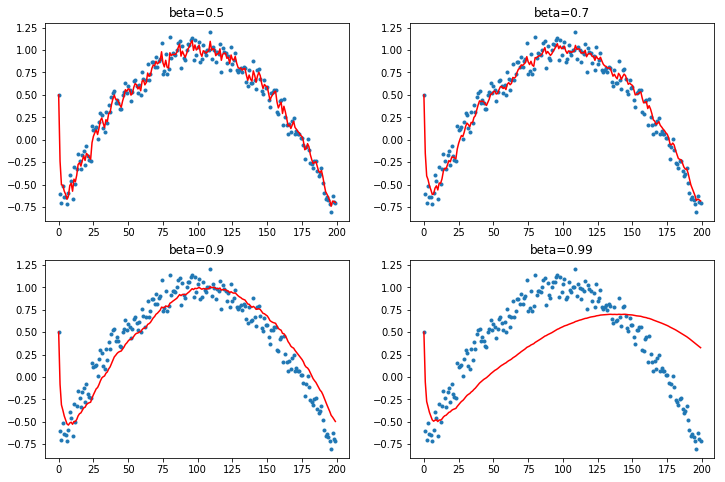
A12. regardless of innate pattern in data, avg follows the current output faster when the momentum is low. However, when the beta gets bigger, it gets stable while too big number does lead to its own way (exploding). It is very interesting to see how it changes w/wo dampening.
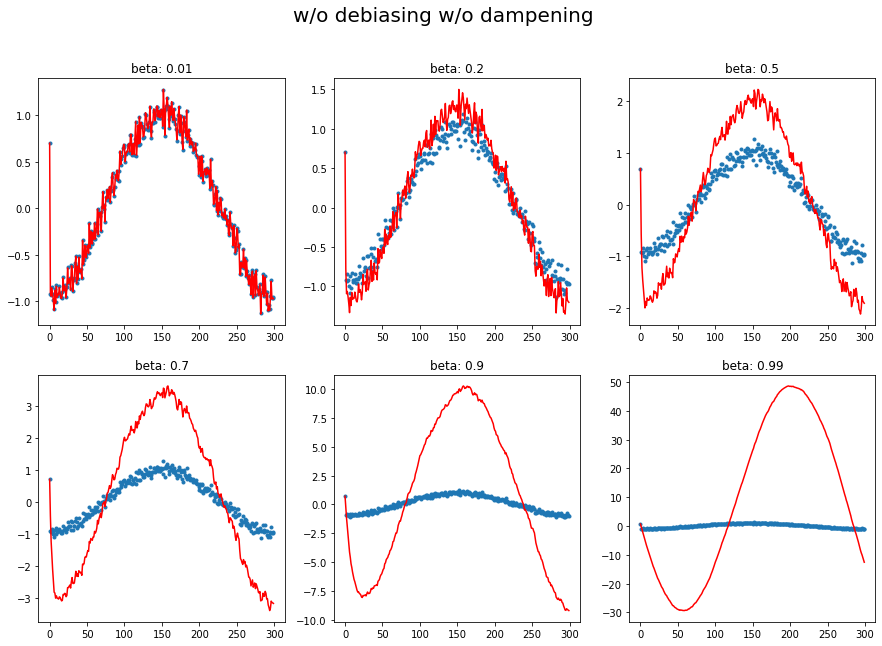
The target function is cosine, with a little random noise.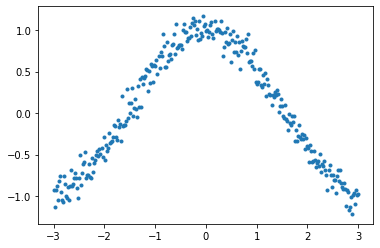 
You can easily observe that large beta (without dampening) responds late, and even hyperbole previous pattern without dampening.
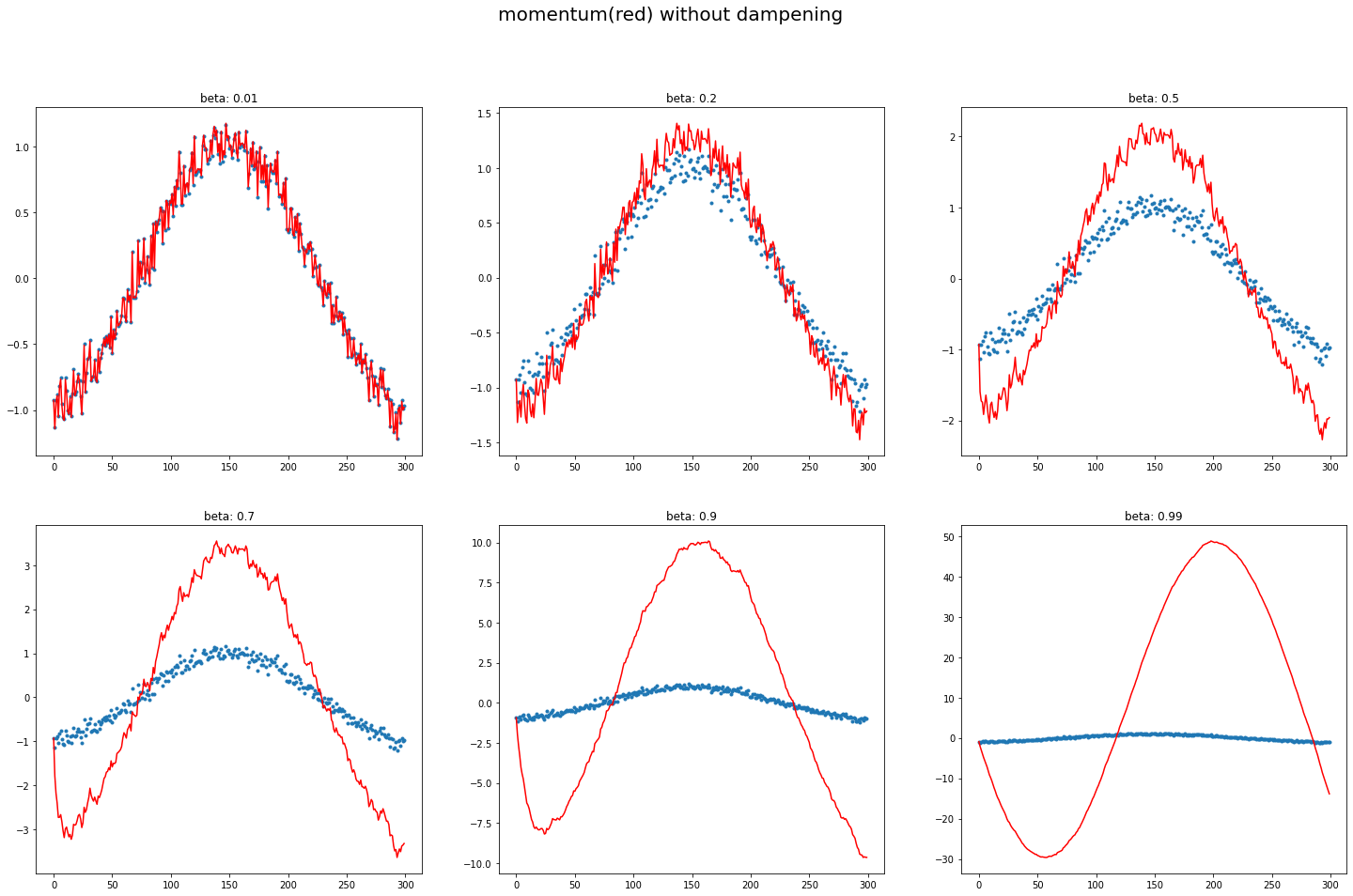
def plot_mom(f, title=''):
beta = [0.01, 0.2, 0.5, 0.7, 0.9, 0.99]
fig, axes = plt.subplots(2,3, figsize=(15,10))
for b, ax in zip(beta, axes.flatten()):
ax.plot(y, linestyle='None', marker='.')
avg, result = 0, []
for i, yi in enumerate(y):
avg, res = f(avg, b, yi, i)
result.append(res)
ax.plot(result, color='red')
ax.set_title(f"beta: {b}")
fig.suptitle(f'{title}', fontsize=20)
def mom1(avg, b, yi, i):
avg = (avg*b + yi)
return avg, avg
plot_mom(mom1, 'w/o debiasing w/o dampening')
def mom2(avg, b, yi, i):
avg = ((avg*b) + (1-b)*yi)
return avg, avg
x = torch.linspace(-3, 3, 300)
y = torch.cos(x) + torch.randn(len(y)) * 0.1
y[0] = 0.7
plt.plot(x, y, linestyle='None', marker='.')
plot_mom(mom1, 'w/o debiasing w/o dampening')
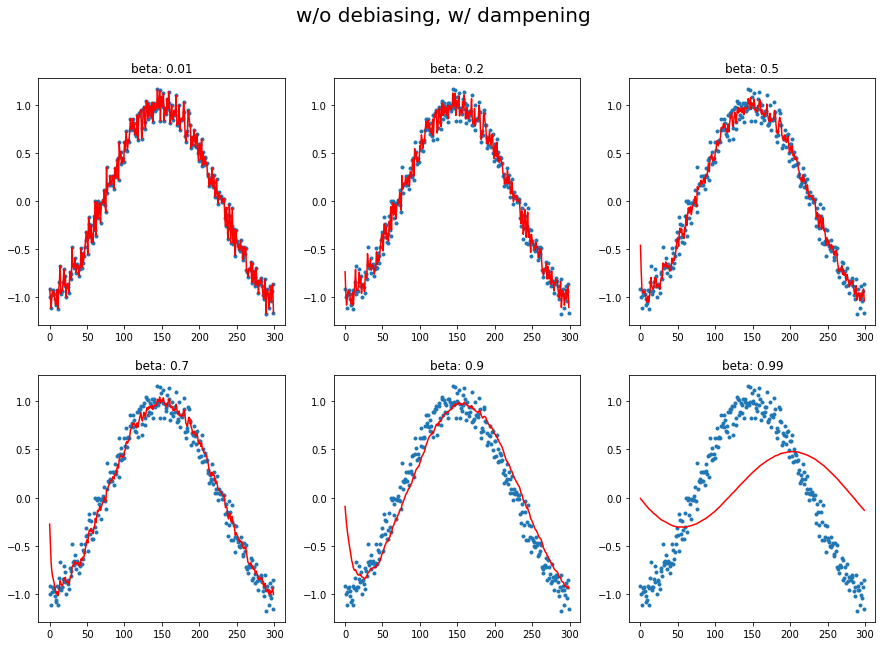
plot_mom(mom2, 'w/o debiasing, w/ dampening')
A13. Debiasing is a trick to correct weird behavior of learning rate in first batch (which is usually defined by initial learinng rate argument when you initlaize optimizer).
We need debiasing as it will help the learning rate quickly adapt to its (ideal) pattern.
Debiasing corresponds to the sum of all coefficients in the moving average, and (……#TODO….do it myself) final result reduces to \(1-\beta^{i+1}\)
def mom3(avg, b, yi, i):
avg = (avg*b + yi)
return avg, avg/(1-b**(i+1))
plot_mom(mom3, 'w/ debiasing, w/o dampening')
def mom4(avg, b, yi, i):
avg = ((avg*b) + (1-b)*yi)
return avg, avg/(1-b**(i+1))
plot_mom(mom4, 'w/ debiasing, w dampening')
A14.
- Adam: (To be done) #TODO
- Adam is the combination of momentum and RMSProp, which was devised by Hinton, 2015, to change trustness of current gradient depending on previous history.
- We need to track
- the moving average of the gradient,
AverageGrad - the moving average of the gradient squared,
AverageSqrGrad - the number of steps done during training for the debiasing, ,
StepCount - the debiasing
adam_stepwhich updates parameter.adam_optwhich groups/bundle the individual objects having its own role of Adam optimizing process.
- the moving average of the gradient,
# for momentum
class AverageGrad(Stat):
_defaults = dict(mom=0.9)
def __init__(self, dampening=False): self.dampening=dampening
def init_state(self, p): return {'grad_avg': torch.zeros_like(p.grad.data)}
def update(self, p, state, mom, **kwargs):
state['mom_damp'] = 1-mom if self.dampening else 1
state['grad_avg'].mul_(mom).add_(state['mom_damp'], p.grad.data)
return state
# for stepsize - RMSProp
class AverageSqdGrad(Stat):
_defaults = dict(sqr_mom=0.9)
def __init__(self, dampening=True): self.dampening=dampening
def init_state(self, p): return {'sqr_avg': torch.zeros_like(p.grad.data)}
def update(self, p, state, sqr_mom, **kwargs):
state['sqr_damp'] = 1-sqr_mom if self.dampening else 1
state['sqr_avg'].mul_(sqr_mom).addcmul_(state['sqr_damp'], p.grad.data, p.grad.data)
return state
class StepCount(Stat):
def init_state(self, p): return {'step':0}
def update(self, p, state, **kwargs):
state['step'] +=1
return state
def debias(mom, damp, step): return damp * (1-mom**step) / (1-mom)
def adam_step(p, lr, mom, mom_damp, step, sqr_mom, sqr_damp, grad_avg, sqr_avg, eps, **kwargs):
debias1 = debias(mom , mom_damp, step)
debias2 = debias(sqr_mom, sqr_damp, step)
p.data.addcdiv_(-lr / debias1, grad_avg, (sqr_avg/debias2).sqrt()+eps)
return p
adam_step._defaults = dict(eps=1e-5)
def adam_opt(xtra_step=None, **kwargs):
return partial(StatefulOptimizer,
steppers=[adam_step, weight_decay]+listify(xtra_step),
stats=[AverageGrad(dampening=True), AverageSqdGrad(), StepCount()], **kwargs)
- Note: Remember example below and that python picks up its keyword arguments and it does duplicate. ``` def getid(p, id, **kwargs): print(f”id: {id}”, f”kwargs: {kwargs}”) def outer(p, **kwargs): getid(p, **kwargs)
outer(10, **{‘lr’:0.1, ‘id’:1234, ‘name’: ‘Jessy’}) ```
Research Journal
- momentum & debiasing
1.a Momentum only
1.b Momentum with dampening
1.c Momentum with debiasing
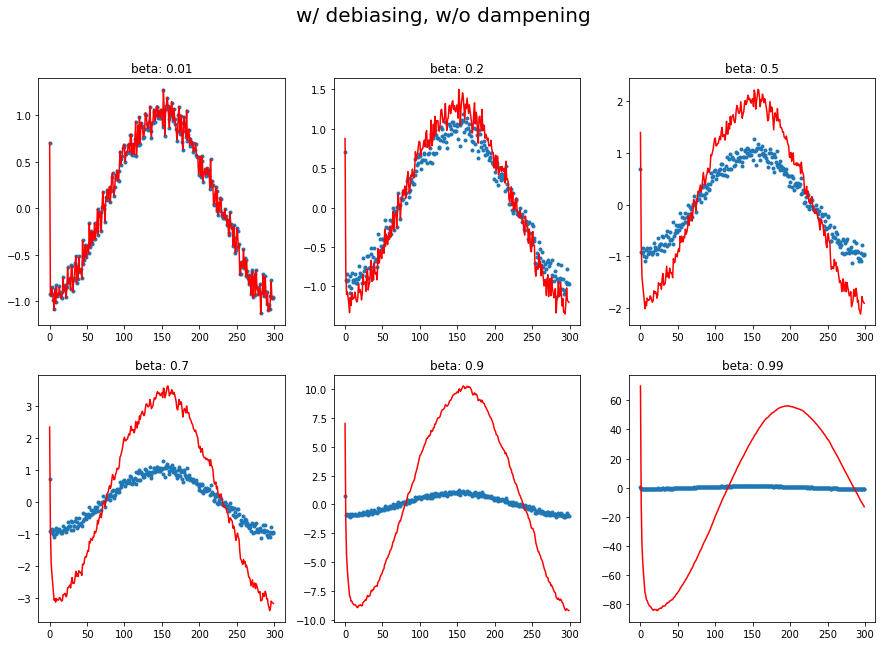
1.d Momentum with dampening and debiasing
- warm-up vs cool-down
-
Can I get a pre-defined positional parameter in **kwargs?
sgd_stepfunction gets two positional parameter, but compose function renders it named **hyper ↩ -
Anyway the purpose of adding to loss is to reflect its derivative to the parameter. So rather than adding it to forward pass, it’s efficient to add it directly to the parameter in optimization phase. ↩
-
However still I’m not sure how this is different from linear interpolation(
lerp) and also I don’t know why Jeremy usedmul_instead oflerp_↩
Part2 lesson 11, 08 datablock | fastai 2019 course -v3