What's inside Pytorch Operator?

This note is divided into 4 section.

Section1: What is the meaning of ‘deep-learning from foundations?’
Section2: What’s inside Pytorch Operator?
Section3: Implement forward&backward pass from scratch
Section4: Gradient backward, Chain Rule, Refactoring

What’s inside Pytorch Operator?

Section02

Time comparison with pure Python

Matmul with broadcasting
> 3194.95 times faster
Einstein summation
> 16090.91 times faster
Pytorch’s operator
> 49166.67 times faster

1. Elementwise op

1.1 Frobenius norm

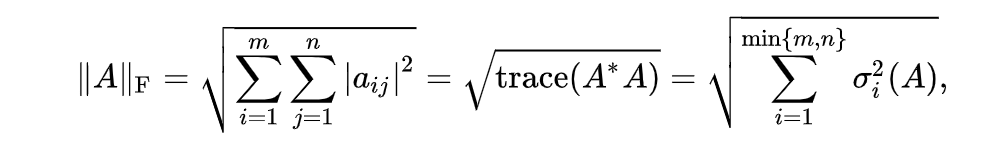
above converted into

(m*m).sum().sqrt()

Plus, don’t suffer from mathmatical symbols. He also copy and paste that equations from wikipedia.
and if you need latex form, download it from archive.

2. Elementwise Matmul

What is the meaning of elementwise?
We do not calculate each component. But all of the component at once. Because, length of column of A and row of B are fixed.
How much time we saved?

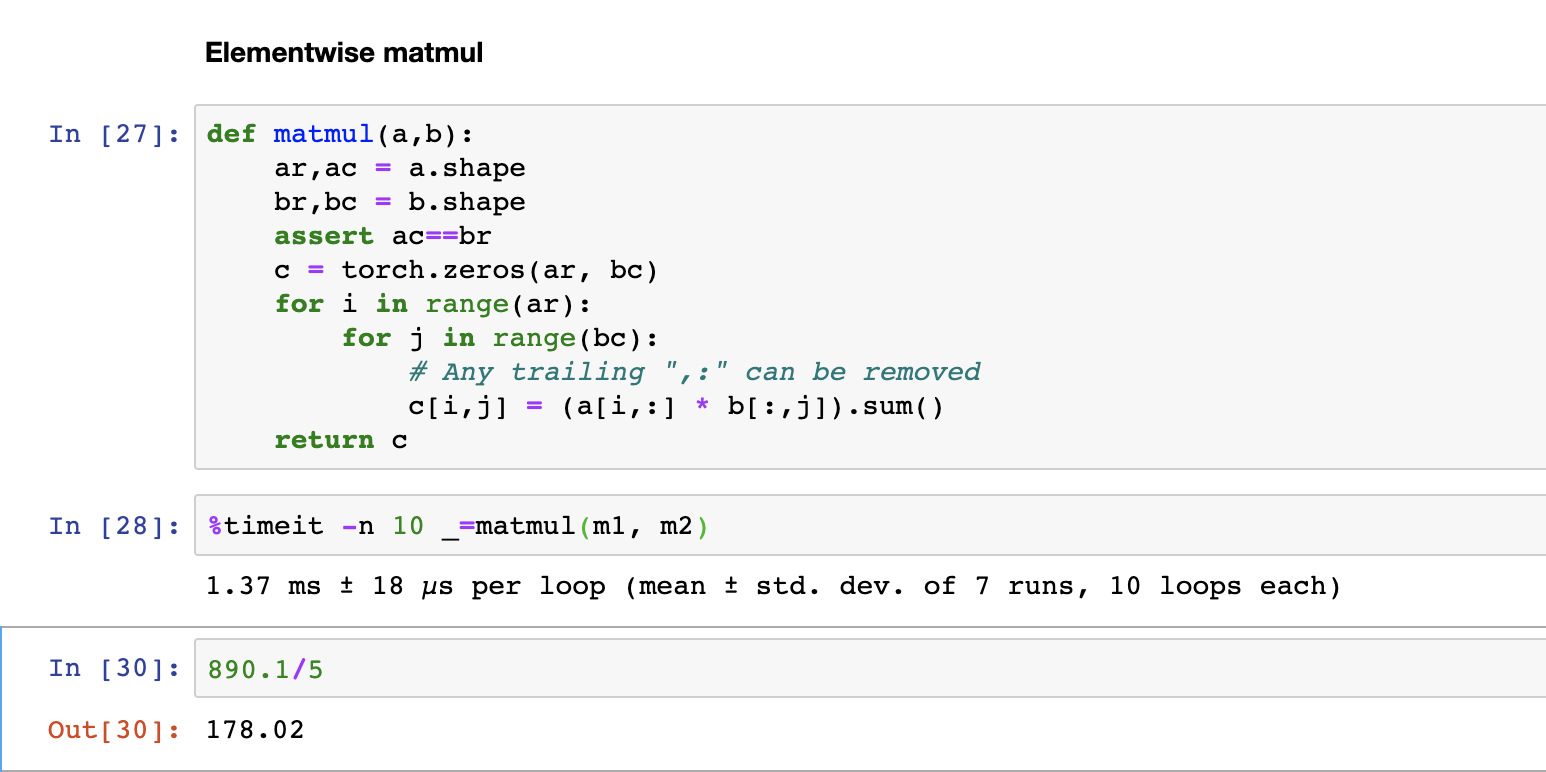
So now that takes 1.37ms. We have removed one line of code and it is a 178 times faster…

#TODO I don’t know where the 5 from. but keep it. Maybe this is related with frobenius norm…? as a result, the code before

for k in range(ac):
    c[i,j] += a[i,k] + b[k,j]

the code after

c[i,j] = (a[i,:] * b[:,j]).sum()

To compare it (result betweet original and adjusted version) we use not test_eq but other function. The reason for this is that due to rounding errors from math operations, matrices may not be exactly the same. As a result, we want a function that will “is a equal to b within some tolerance”

#export
def near(a,b): 
    return torch.allclose(a, b, rtol=1e-3, atol=1e-5)

def test_near(a,b): 
    test(a,b,near)

test_near(t1, matmul(m1, m2))

3. Broadcasting

Now, we will use the broadcasting and remove

c[i,j] = (a[i,:] * b[:,j]).sum()

How it works?

>>> a=tensor([[10,10,10],
          [20,20,20],
          [30,30,30]])
>>> b=tensor([1,2,3,])

>>> a,b
    
(tensor([[10, 10, 10],
         [20, 20, 20],
         [30, 30, 30]]),
tensor([1, 2, 3]))
         

>>> a+b

tensor([[11, 12, 13],
        [21, 22, 23],
        [31, 32, 33]])

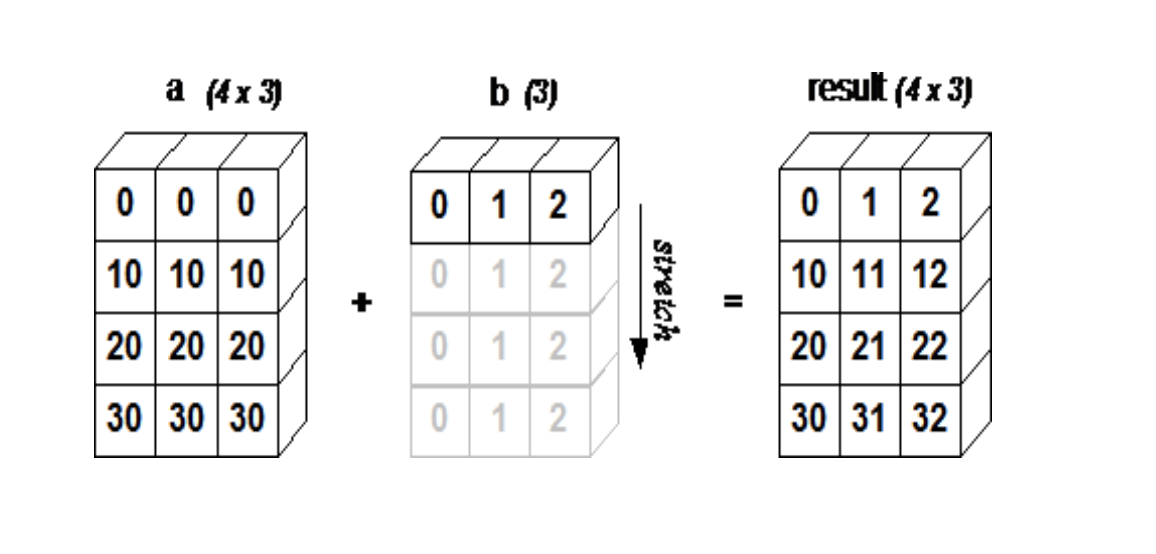
<Figure 2> demonstrated how array b is broadcasting(or copied but not occupy memory) to compatible with a. Refered from numpy_tutorial

there is no loop, but it seems there is exactly the loop.
This is not from jeremy (actually after a moment he cover it) but i wondered How to broadcast an array by columns?

c=tensor([[1],[2],[3]])
a+c

tensor([[11, 11, 11], [22, 22, 22], [33, 33, 33]])s

What is tensor.stride()?

help(t.stride)

Help on built-in function stride:
stride(…) method of torch.
Tensor instance
stride(dim) -> tuple or int
Returns the stride of :attr:’self’ tensor.
Stride is the jump necessary to go from one element to the next one in the specified dimension :attr:’dim’.
A tuple of all strides is returned when no argument is passed in.
Otherwise, an integer value is returned as the stride in the particular dimension :attr:’dim’.

Args: dim (int, optional): the desired dimension in which stride is required Example::*

x = torch.tensor([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])`
x.stride()
>>> (5, 1)
x.stride(0)
>>> 5
x.stride(-1)
>>> 1

unsqueeze & None index
We can manipulate rank of tensor
Special value ‘None’, which means please squeeze a new axis here
== please broadcast here

c = torch.tensor([10,20,30])
c[None,:]

in c, squeeze a new axis in here please.

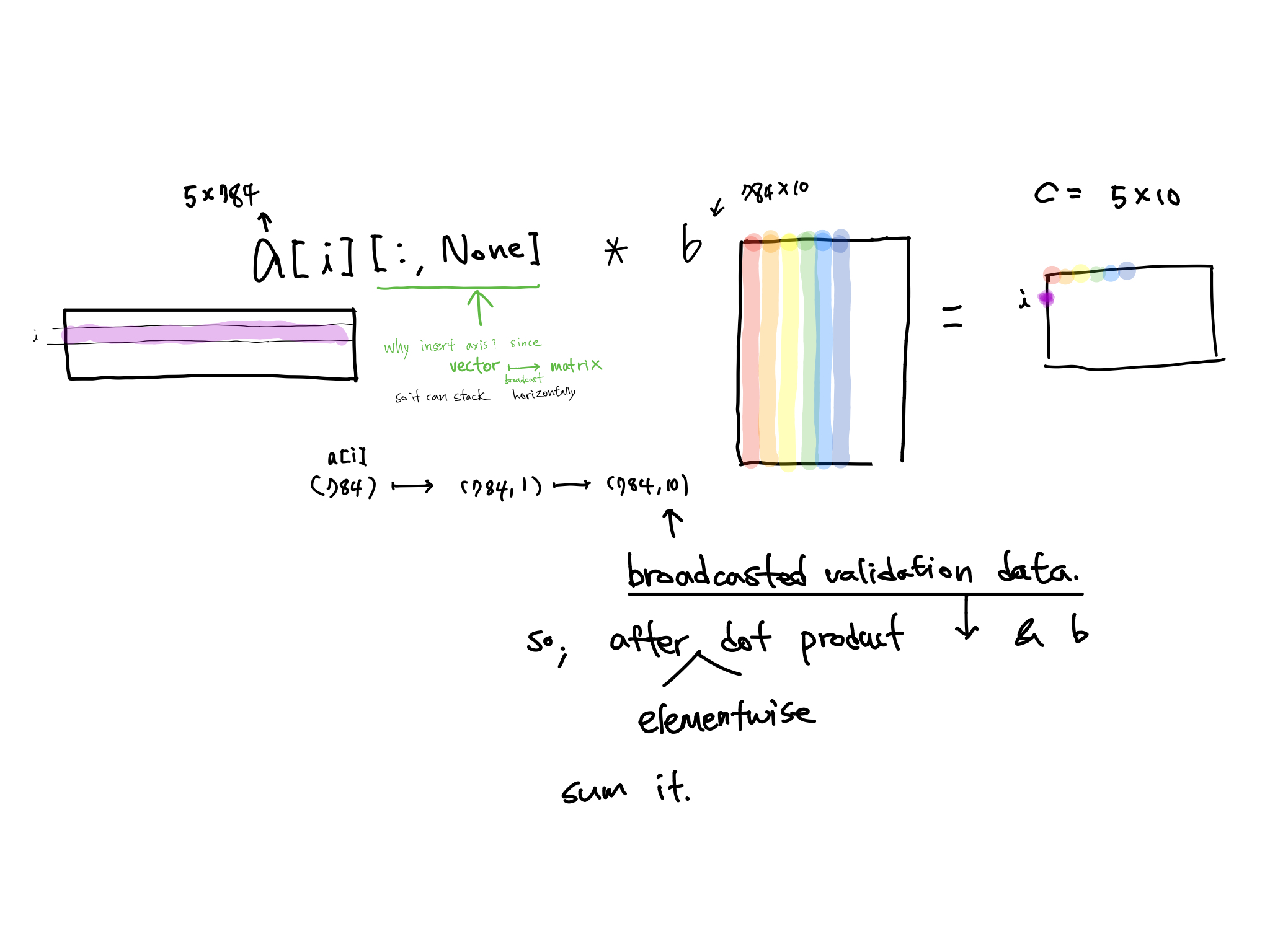
2.2 Matmul with broadcasting

for i in range(ar):
#   c[i,j] = (a[i,:]).          *[:,j].sum() #previous
    c[i]   = (a[i].unsqueeze(-1) * b).sum(dim=0)

And Using None also (As howard teached)

c[i]   = (a[i  ].unsqueeze(-1) * b).sum(dim=0) #howard
c[i]   = (a[i][:,None] * b).sum(dim=0) # using None
c[i]   = (a[i,:,None]*b).sum(dim=0)

⭐️Tips🌟
1) Anytime there’s a trailinng(final) colon in numpy or pytorch you can delete it ex) c[i, :] = c [i] 2) any number of colon commas at the start, you can switch it with the single elipsis. ex) c[:,:,:,:,i] = c […,i]

2.3 Broadcasting Rules

What if we tensor.size([1,3]) * tensor.size([3,1])?
```
torch.Size([3, 3])
```
What is scale????
What if they are one array is times of the other array?
ex) Image : 256 x 256 x 3
Scale : 128 x 256 x 3
Result: ?
Why I did not inserted axis via None, but happened broadcasting?

>>> c * c[:,None]
tensor([[100., 200., 300.],
        [200., 400., 600.],
        [300., 600., 900.]])

maybe it broadcast cz following array has 3 rows

as same principle, no matter what nature shape was, if we do the operation tensor broadcasts to the other.

>>> c==c[None]
tensor([[True, True, True]])

>>> c[None]==c[None,:]
tensor([[True, True, True]])

>>>c[None,:]==c
tensor([[True, True, True]])

3. Einstein summation

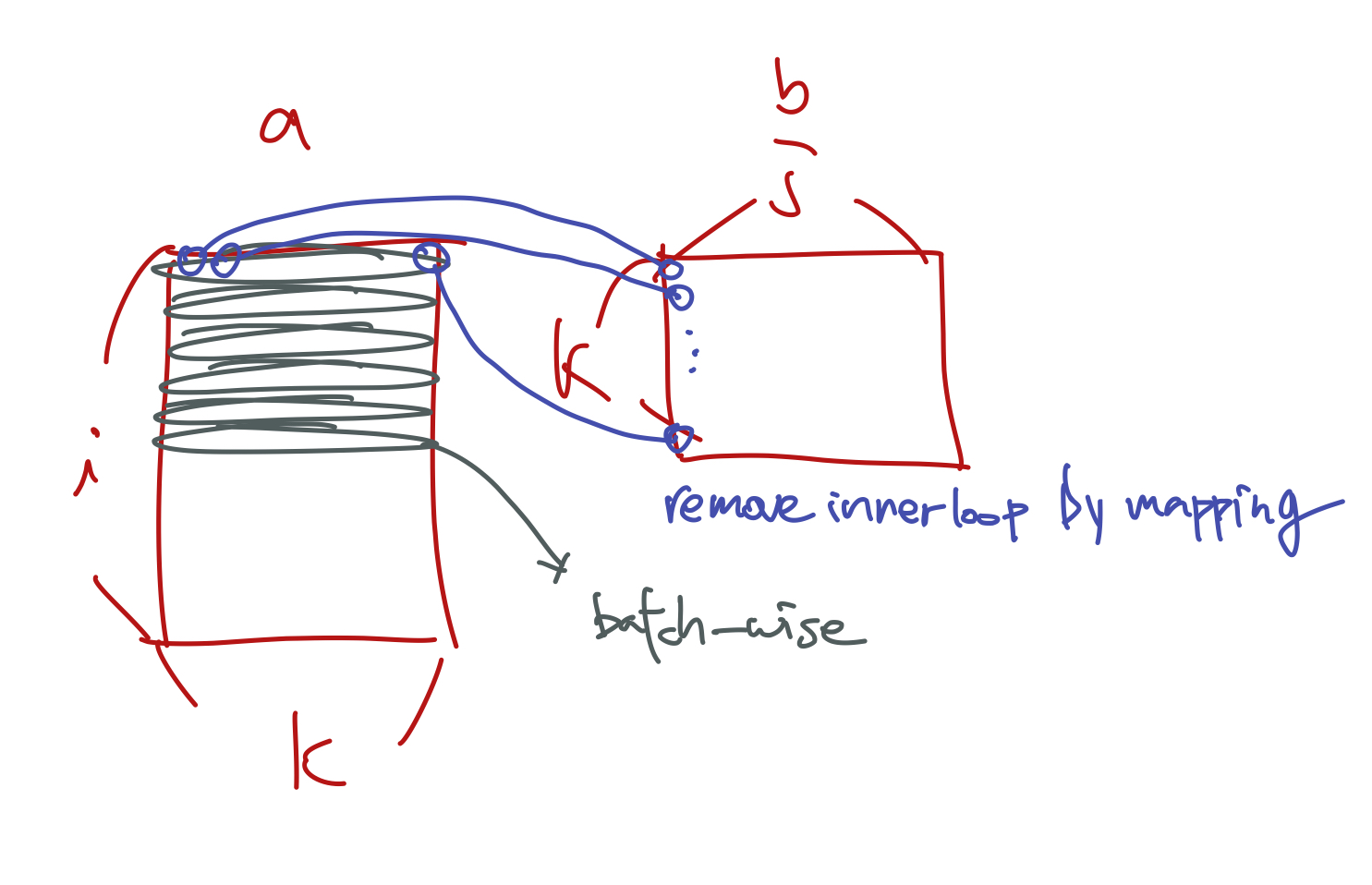
Creates batch-wise, remove inner most loop, and replaced it with an elementwise product a.k.a

c[i,j] += a[i,k] * b[k,j]

inner most loop

c[i,j] = (a[i,:] * b[:,j]).sum()

elementwise product

Because K is repeated so we do a dot product. And it is torch.

Usage of einsum() 1) transpose 2) diagnalisation tracing 3) batch-wise (matmul)

…

einstein summation notation

def matmul(a,b): return torch.einsum('ik,kj->ij', a, b)

so after all, we are now 16000 times faster than Python.

4. Pytorch op

49166.67 times faster than pure python

And we will use this matrix multiplication in Fully Connect forward, with some initialized parameters and ReLU.

But before that, we need initialized parameters and ReLU,

Footnote

Resources

Frobenius Norm Review
Broadcasting Review (especially Rule)
- Refer colab! (I totally confused with extension of arrays)
torch.allclose Review
np.einsum Review