Gradient backward, Chain Rule, Refactoring

This note is divided into 4 section.
- Section1: What is the meaning of ‘deep-learning from foundations?’
- Section2: What’s inside Pytorch Operator?
- Section3: Implement forward&backward pass from scratch
- Section4: Gradient backward, Chain Rule, Refactoring

” Lecture 08 - Deep Learning From Foundations-part2 “

Homework

Foundation version
- Gradients backward pass
Refactor model

Forward process

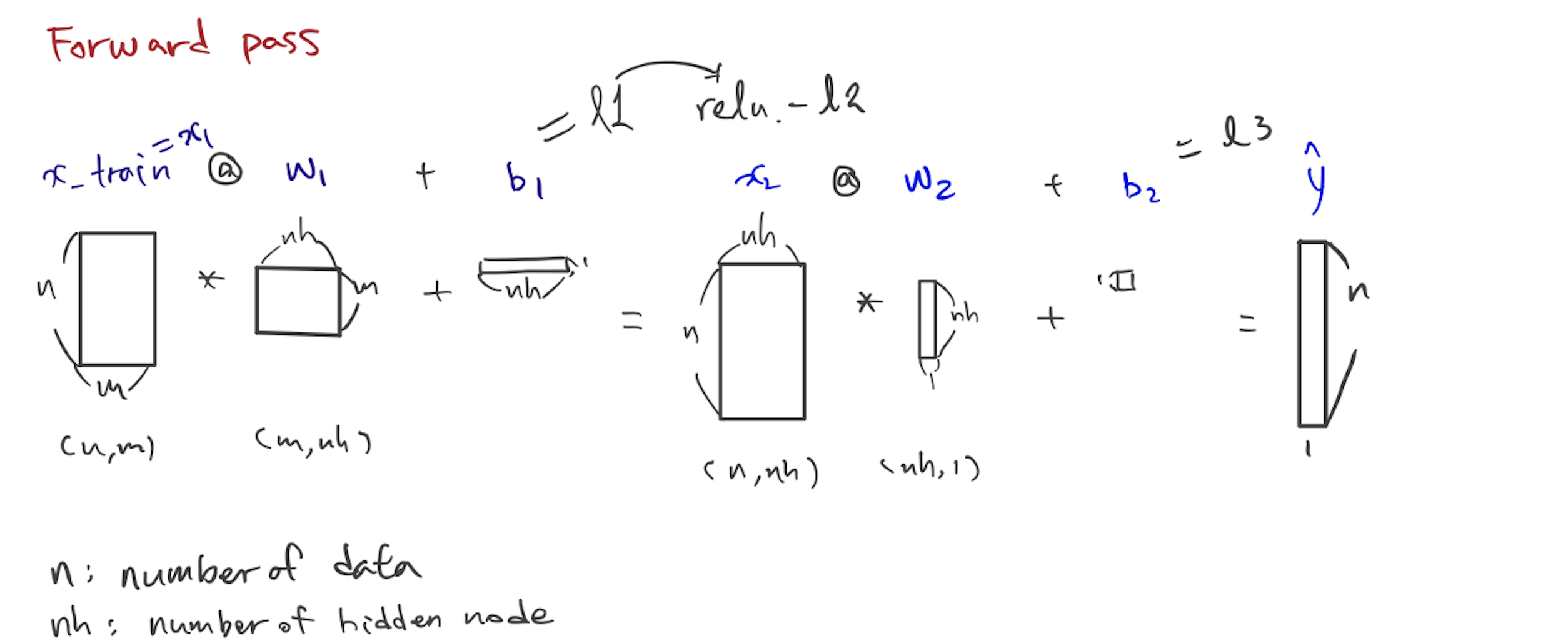
Foundation version

Gradients backward pass

Gradients is output with respect to parameter
we’ve done this work in this path(below)

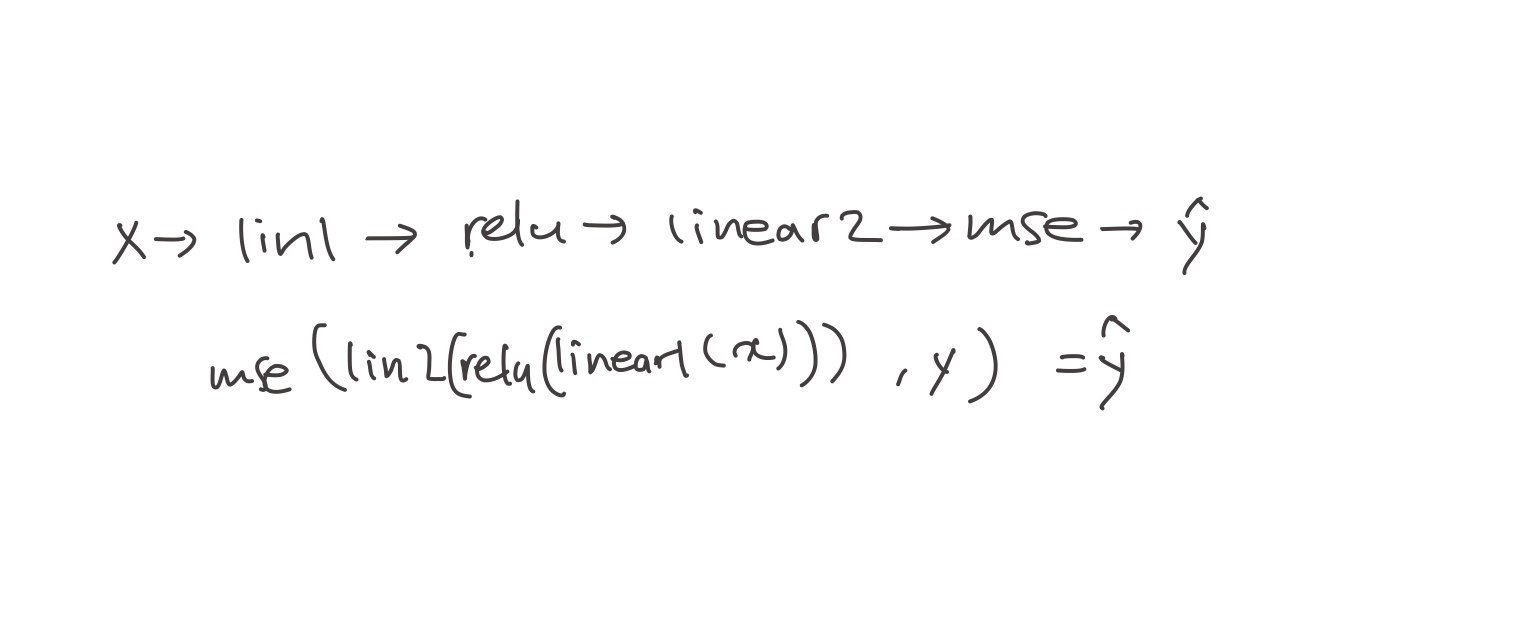
to simplify this calculus, we can just change it into

$y=f(u)$, $u=g(x)$

So, you should know of the derivative of each bit on its own, and then you multiply them all together. As a result, it would be $dy$ over $dx$ cross over the data.

So you can get gradient, output with respect to parameter

What order should we calculate?

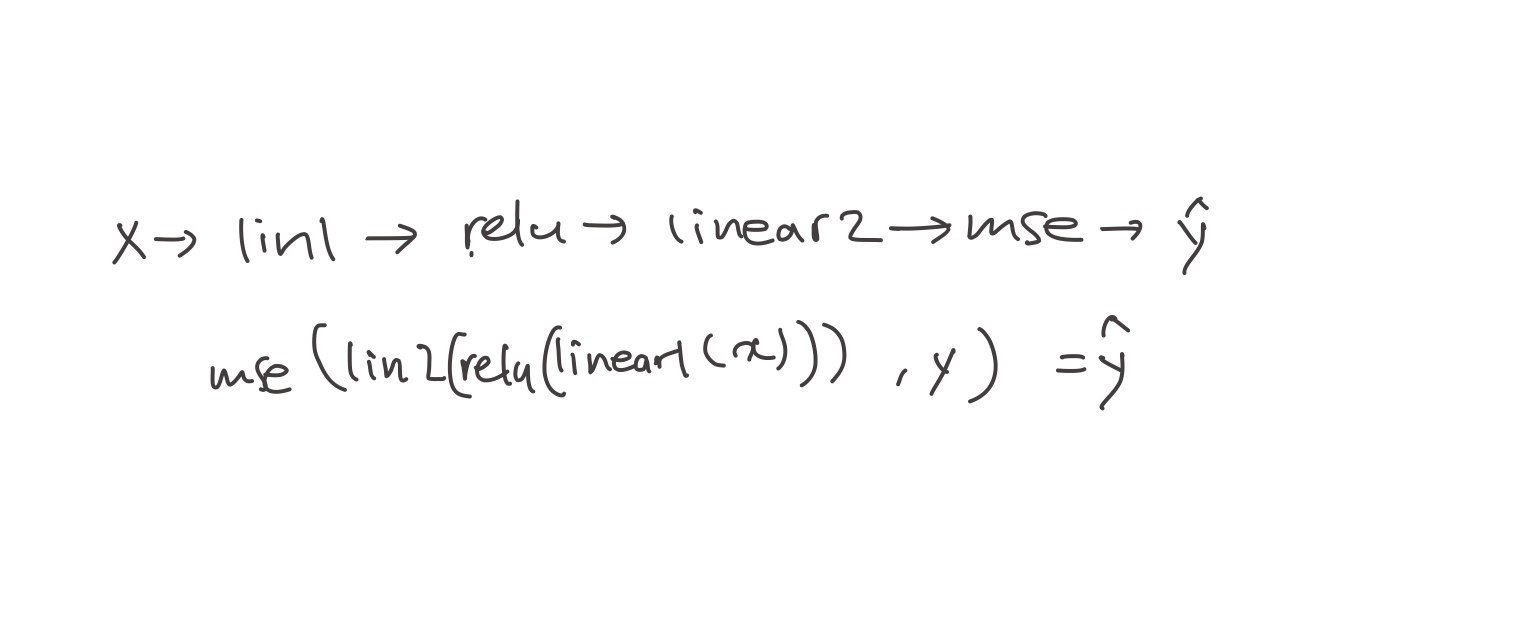
BTW, why Jeremy wrote $\hat y$ , not Loss function?¹

decompose function

We want to get derivative of $w_1$ which forms $t=x_1 @ w_1 + b_1$
But, we have a estimation of answer (we call it y hat) now
So, I will decompose funciton to trace target variable.

\[\overset{\rightharpoonup}{u}\ \ linear_1\ \ \overset{\rightharpoonup}{w}\ \ ReLU\ \ \overset{\rightharpoonup}{v}\ \ linear_2\ \ \overset{\rightharpoonup}{a}\ \ MSE = \hat y\]

Using the above forward pass, we can suppose some function from the end.
start from $\hat y$ , We know MSE funciton got two parameters, output, $u$ and target $y$ .
from MSE’s input we know $linear_2$ function’s output and supposing v is input of that function, $linear_2(v) = u$
similarly, v became output of $ReLU, ReLU(t) = v$

chain rule with code

examplify backward process by random sampling
To get a variable, I modified forward model a little

def model_ping(out = 'x_train'):
    l1 = lin(x_train, w1, b1) # one linear layer
    l2 = relu(l1) # one relu layer
    l3 = lin(l2, w2, b2) # one more linear layer
    return eval(out)

Be careful we don’t use mse_loss in backward process

1) start with the very last function, which is loss funciton. MSE

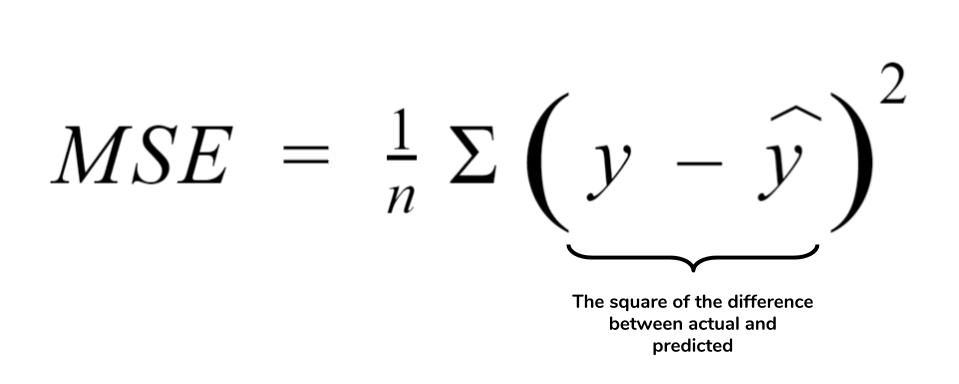
\[\color{red}{\frac{\partial}{\partial u}MSE(u,y)} \times\frac{\partial}{\partial v}l_2(v)\times\frac{\partial}{\partial t}ReLU(t)\times\frac{\partial}{\partial x}l_1(x)\]

If we codify this formula,

def mse_grad(inp, targ):  #mse_input(1000,1), mse_targ (1000,1)
    # grad of loss with respect to output of previous layer
    inp.g = 2. * (inp.squeeze() - targ).unsqueeze(-1) / inp.shape[0]

And, this can be examplified like below.
Notice that input of gradient function is same with forward function

y_hat = model_ping('l3') #get value from forward model
y_hat.g = ((y_hat.squeeze(-1)-y_train).unsqueeze(-1))/y_hat.shape[0]

y_hat.g.shape
>>> torch.Size([50000, 1])

We can just calculate using broadcasting, not using squeeze. then why should do and unsqueeze again?
🎯 It’s related with random access memory(RAM).. If I don’t squeeze, (I’m using colab) it out of RAM.

2) Derivative of linear2 function

\[\frac{\partial}{\partial u}MSE(u,y) \times\color{red}{\frac{\partial}{\partial v}l_2(v)} \times \frac {\partial}{\partial t}ReLU(t)\times\frac{\partial}{\partial x}l_1(x)\]

This process’s weight dimensions defined by axis=1, axis=2.
axis=0 dimension means size of data. This will be summazed by .sum(0) method.
unsqeeze(-1)&unsqeeze(1) seperates the dimension, and make a dot product, and vanish axis=0 dimension.

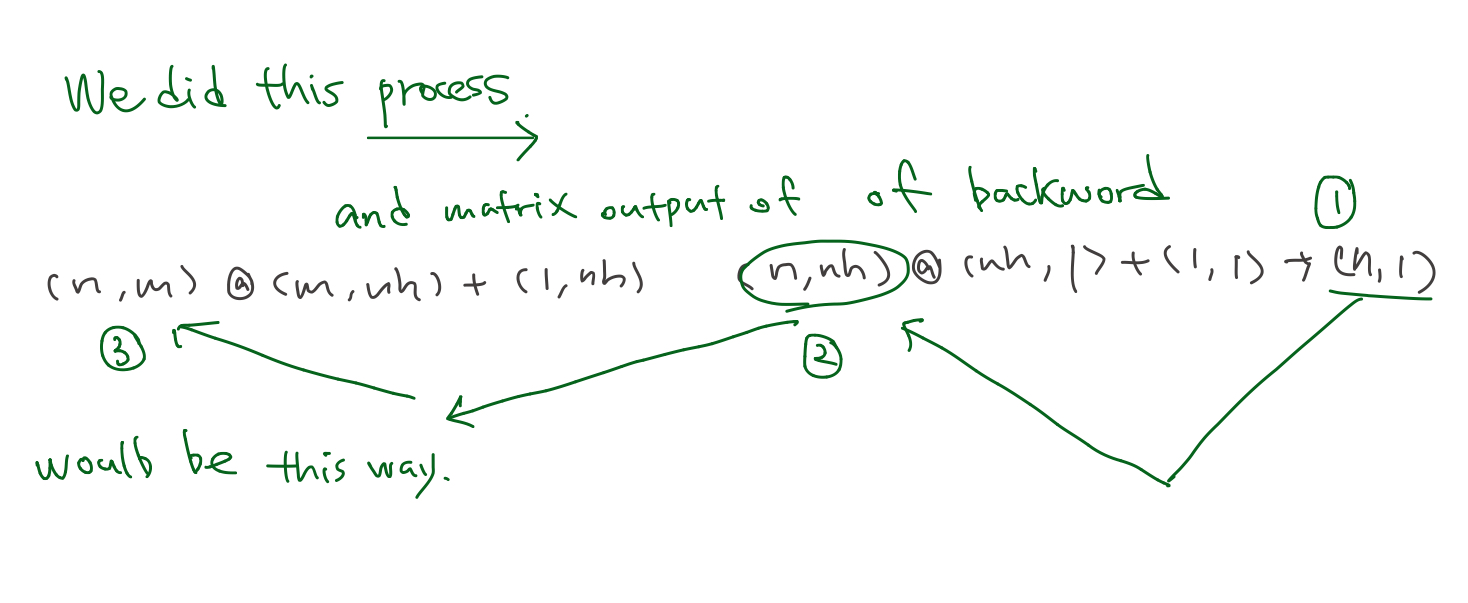
def lin_grad(inp, out, w, b):
    # grad of matmul with respect to input
    inp.g = out.g @ w.t()
    w.g = (inp.unsqueeze(-1) * out.g.unsqueeze(1)).sum(0)
    b.g = out.g.sum(0)

Examplified below

lin2 = model_ping('l2'); #get value from forward model
lin2.g = y_hat.g@w2.t(); 
w2.g = (lin2.unsqueeze(-1) * y_hat.g.unsqueeze(1)).sum(0);
b2.g = y_hat.g.sum(0);

lin2.g.shape, w2.g.shape, b2.g.shape
>>> torch.Size([50000, 50])torch.Size([50, 1])torch.Size([1])

Notice going reverse order, we’re passing in gradient backward

3) derivative of ReLU

\[\frac{\partial}{\partial u}MSE(u,y) \times \frac{\partial}{\partial v}l_2(v) \times \color{red}{\frac{\partial}{\partial t}ReLU(t)}\times\frac{\partial}{\partial x}l_1(x)\]

def relu_grad(inp, out):
    # grad of relu with respect to input activations
    inp.g = (inp>0).float() * out.g

Examplified below

lin1=model_ping('l1') #get value from forward model
lin1.g = (lin1>0).float() * lin2.g;
lin1.g.shape
>>> torch.Size([50000, 50])

4) Derivative of linear1

Same process with 2) but, this process’s weight has

\[\frac{\partial}{\partial u}MSE(u,y) \times \frac{\partial}{\partial v}l_2(v) \times \frac{\partial}{\partial t}ReLU(t)\times\color{red}{\frac{\partial}{\partial x}l_1(x)}\]

def lin_grad(inp, out, w, b):
    # grad of matmul with respect to input
    inp.g = out.g @ w.t()
    w.g = (inp.unsqueeze(-1) * out.g.unsqueeze(1)).sum(0)
    b.g = out.g.sum(0)

Examplified below

x_train.g = lin1.g @ w1.t(); 
w1.g = (x_train.unsqueeze(-1) * lin1.g.unsqueeze(1)).sum(0); 
b1.g = lin1.g.sum(0);

x_train.g.shape, w1.g.shape, b1.g.shape
>>> torch.Size([50000, 784])torch.Size([784, 50])torch.Size([50])

5) Then it goes backward pass

def forward_and_backward(inp, targ):
    # forward pass:
    l1 = inp @ w1 + b1
    l2 = relu(l1)
    out = l2 @ w2 + b2
    # we don't actually need the loss in backward!
    loss = mse(out, targ)
    
    # backward pass:
    mse_grad(out, targ)
    lin_grad(l2, out, w2, b2)
    relu_grad(l1, l2)
    lin_grad(inp, l1, w1, b1)

Version 1 (Basic)- Wall time: 1.95 s

Summary

Notice that output of function at forward pass became input of backward pass
backpropagation is just the chain rule
value loss (loss=mse(out,targ)) is not used in gradient calcuation.
- Because, it doesn’t appear with the weight.
w1g, w2g, b1g, b2g, ig will be used for optimizer

check the result using Pytorch autograd

require_grad_ is the magical function, which can automatic differentiation.²
- This magical auto gradified tensor keep track what happend in forward (taking loss function),
- and do the backward³
- So it saves our time to differentiate ourselves
Postfix underscore means in pytorch, in-place function, What is in-place function?

⤵️ THis is benchmark…..

Version 2 (torch autograd)- Wall time: 3.81 µs

Refactor model

Amazingly, just refactoring our main pieces, it comes down up to Pytorch package.

🌟 Implement yourself, Practice, practice, practice! 🌟

Layers as classes

Relu and Linear are layers in oue neural net. -> make it as classes
For the forward, using __call__ for the both of forward & backward. Because ‘call’ means we treat this as a function.

class Lin():
    def __init__(self, w, b): self.w,self.b = w,b
        
    def __call__(self, inp):
        self.inp = inp
        self.out = inp@self.w + self.b
        return self.out
    
    def backward(self):
        self.inp.g = self.out.g @ self.w.t()
        # Creating a giant outer product, just to sum it, is inefficient!
        self.w.g = (self.inp.unsqueeze(-1) * self.out.g.unsqueeze(1)).sum(0)
        self.b.g = self.out.g.sum(0)

Remember that in lin_grad function, we save bias&weight!!!!!

💬 inp.g : gradient of the output with respect to the input. {: style=”color:grey; font-size: 90%; text-align: center;”}
💬 w.g : gradient of the output with respect to the weight. {: style=”color:grey; font-size: 90%; text-align: center;”}
💬 b.g : gradient of the output with respect to the bias. {: style=”color:grey; font-size: 90%; text-align: center;”}

class Model():
    def __init__(self, w1, b1, w2, b2):
        self.layers = [Lin(w1,b1), Relu(), Lin(w2,b2)]
        self.loss = Mse()
        
    def __call__(self, x, targ):
        for l in self.layers: x = l(x)
        return self.loss(x, targ)
    
    def backward(self):
        self.loss.backward()
        for l in reversed(self.layers): l.backward()

refer to Jeremy’s Model class, he put layers in list
Dionne’s self-study note: Decomposing Jeremy’s Model class
1. init needs weight, bias but not x data
2. when call that class(a.k.a function) it gave x data and y label!
3. jeremy composited function in layers. x = l(x) so concise…..
4. also utilized that layer list when backward ust reversing it (using python list’s method)
And he is recursively calling the function on the result of the previous thing. ⬇️

for l in self.layers:
    x = l(x)

Q2: Don’t I need to declare magical autograd function, requires_grad_?{: style=”color:red; font-size: 130%; text-align: center;”}

[The questions migrated to this article]

Version 3 (refactoring - layer to class)- Wall time: 5.25 µs

Modue.forward()

Duplicate code makes execution time slow.
- Role of __call__ changed. No more __call__ for implementing forward pass.
- By initializing the forward with __call__, Module.forward() use overriding to maximize reusability. So any layer inherit Module, can use parent’s function.

gradient of the output with respect to the weight

(self.inp.unsqueeze(-1) * self.out.g.unsqueeze(1)).sum(0)

can be reexpressed using einsum,

torch.einsum("bi,bj->ij", inp, out.g)

Defining forward and Module enables Pytorch to out almost duplicates

Version 4 (Module & einsum)- Wall time: 4.29 µs

Q2: Isn’t there any way to use broadcasting? Why we should use outer product?{: style=”color:red; font-size: 130%; text-align: center;”}

Without einsum

Replacing einsum to matrix product is even more faster.

torch.einsum("bi,bj->ij", inp, out.g)

can be reexpressed using matrix product,

inp.t() @ out.g

Version 5 (without einsum)- Wall time: 3.81 µs

nn.Linear and nn.Module

Torch’s package nn.Linear and nn.Module

Version 6 (torch package)- Wall time: 5.01 µs

Final, Using torch.nn.Linear & torch.nn.Module ~~~python

class Model(nn.Module): def init(self, n_in, nh, n_out): super().init() self.layers = [nn.Linear(n_in,nh), nn.ReLU(), nn.Linear(nh,n_out)] self.loss = mse

def __call__(self, x, targ):
    for l in self.layers: x = l(x)
    return self.loss(x.squeeze(), targ)

class Model(): def init(self): self.layers = [Lin(w1,b1), Relu(), Lin(w2,b2)] self.loss = Mse()

def __call__(self, x, targ):
    for l in self.layers: x = l(x)
    return self.loss(x, targ)

def backward(self):
    self.loss.backward()
    for l in reversed(self.layers): l.backward()        

~~~